The impedance of a connection i used in the connection choice in a time interval a is calculated as follows.
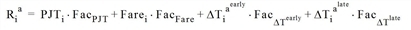
Optionally, each skim value which goes in the impedance can be individually Box-Cox transformed. This does not affect the actual choice model. Any utility function can thus still be applied to the total impedance even when using the Box-Cox transformation.
The impedance calculation is not linked to the actual connection choice, that is, even when calculating the Box-Cox transformation, Logit does not necessarily have to be used. Any other utility function can be selected instead.
The impedance calculation is as follows:
For i = 1, ..., n are xi the different path attributes. Here, the first m of them without restrictions are to be Box-Cox-transformed (namely each into parameter λi). βi stands for the corresponding coefficients. Then the following applies
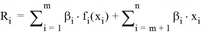
where
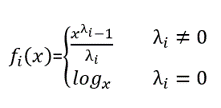
By including this impedance in one of the distribution models Kirchhoff, Logit, Box-Cox or Lohse (Distribution models in the assignment), Visum then determines the utility of a connection in a given time interval and ultimately its percentage of the demand for this interval. The independence can also be included in the distribution rule, if required (Independence of connections).
As before, the proportion of a connection i of the total demand is calculated as follows:
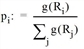
Here, g is the selected utility function (always antitonic). In the case of Logit thus g(x) = e-bx applies.
|
Notes: As can be seen from the definition, when using the Box-Cox transformation for xi generally xi ≥ 0 needs to apply. In case of λi = 0, even xi > 0 needs to be true. If this rule is violated during the run time, the assignment is terminated with an error message. Due to a Box-Cox transformation or caused by negative coefficients, Ri itself can be negative. In that case, only the Logit utility function can be used, otherwise the assignment is terminated with an error message. |